|
|
4.2. On-line method for polynomials
An on-line algorithm
for computing a located real root of a n-degree polynomial with real coefficients can be developed
by simply modifying the newly proposed basic method from the previous section.
For the polynomial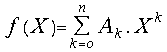
, where
;
we accept all the definitions introduced in the previous
section. Some new values related to the on-line representation of the coefficients
must be added. Let
for all 
(the precision of the coefficients is not specified). We define the
on-line representation of the coefficient
as:
(26)
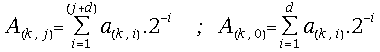,where the digits
belong to the redundant digit set {-1, 0, 1} and d is the
on-line delay.
After completing the j-th iteration step we have computed the following values:
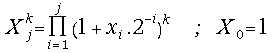and
;
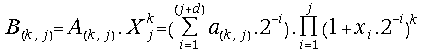for all
.
Recurrence equations
for 
and
can be derived easily:
(26)
=
=
;
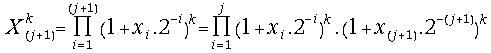(27)
=
=
=
=
=
=
=
=
;
.
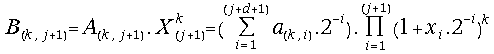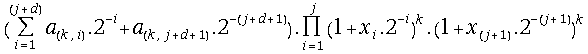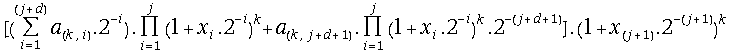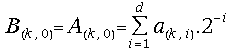By the end of the (j+1)-th iteration step we can compute the value:
(28)
.
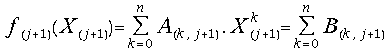As usually we assume the existence of a selection
rule
such that if
, then 
. Of course 
and then 
is the root of the polynomial 
. The natural choice is the standard radix-2 SRT-division-type selection
rule [25] described for the basic method in the previous
section.
We propose a
maximally parallel scheme for the computation of 
thus assuring a minimal time to accumulate the sum (28) no matter
how much area-consuming such a scheme could be. The computations of 
for all k,
are performed simultaneously and according to (27) each of them
can be subdivided into several consecutive stages. Each stage involves a shift
operation followed by a (possibly carry-save) addition of two numbers. Namely
can be evaluated according to
(27) as follows:
(29)
;
;
;
. . . . . . . . . . . . . . . . . . . . . . . .
.
Thus we have
a chain of (k+1) shift-and-add operations starting with
and ending with 
. In accordance with (26) the values of for all
can be computed in a similar way:
(30)
;
;
. . . . . . . . . . . . . . . . . . . . . . . . .
.
Next we shall
describe briefly how to organize overlapping of the computations defined by
(28), (29) and (30) within each iteration step. Suppose we have n Basic
shift-and-add Units (BU). Every basic unit BU has two parallel inputs for operands.
On entering the first input the operand is shifted to the right (the direction
of the less significant digits) at a variable number of digit positions, depending
on the number of the iteration step. After latching the shifted first operand
is added to the second operand coming from the second input of BU. There is
a correspondence between the BU's and the values 
( notice that 
is not included ). We number the BU's from 1 to n to match
the subscripts of. We shall need a separate adder 
to accumulate the sum (28).
Before initializing
the (j+1)-th iteration step all the (j+d+1)-th digits
of the polynomial coefficients
are at our disposal. This is guaranteed by the definition of the on-line algorithm.
So the computation of all 
according to (29) can start at the first stage in the BU's:
.
After the first
stage's completion the second stage for the computation of
immediately follows. At the end of the second stage BU1
outputs the value:
Notice that
after computing 
BU1 is free to be used for another task starting from the third
stage. So we can compute 
in accordance with (30) in BU1.
During the third stage:
-the sum 
can be computed in the separate adder.
Notice that there is no need in an addition operation to form
from
. The newly arrived digit
is simply inserted into its place.
- The first
unit BU1 switches to computation of
:
;
-the units from
BU2 to BUn proceed with computing 
. At the end of the third stage BU2 produces
and becomes available for another task.
Similarly during the fourth stage the following actions are performed simultaneously:
- accumulation
of the sum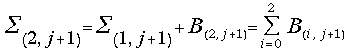
;
- BU1 keeps
on computing:
;
- BU2 starts
the computation of
:
;
- the units
from BU3 to BUn go on with the computation of .
At the end of
the fourth stage 
is accomplished and BU3 is free to switch to 
during the next stage.
By the end of
the (n+1)-th stage BUn finishes the computation of
.
And finally at the end of the (n+2)-th stage the separate adder completes the accumulation of the sum:
and the units from BU1 to BUn produce simultaneously the
values but in a reversed order, i.e.
from to
. Notice that all the Basic shift-and-add Units ( BU's) are kept
busy at all stages during the whole iteration step.
In order to have an on-line output of the
algorithm the computed value of the root
must be digitalized as proposed in [11]. The digitalization procedure is implemented as a SRT-division
of the partial products representing the root by a devisor equal to 1. The quotient
of this division is the digitalized root with digits
belonging to the set {-1, 0, 1}. Before
starting the digitalization procedure we have accumulated the value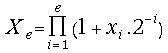
, where e characterizes the on-line
delay. We define residuals
:
;
;
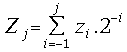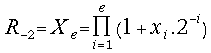, where j = -2,-1, 0, 1, 2, ...
As usually
and finally:
;
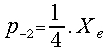; j = -2,-1, 0, 1, 2, ....
.
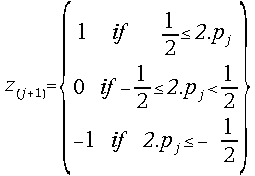The full value
of the on-line delay is formed by two constituents: we must wait for d cycles
before starting the computation of 
and after that another e cycles (iteration steps) must be
accomplished before initializing the digitalization procedure, so the total
on-line delay of the algorithm is (d+e) .
