|
|
4. On-line computation of a located root of a polynomial with real coefficients
4.1. New basic method for polynomials
Our decision to propose a new method for computing roots of polynomials is completely motivated by the key role the polynomials play in algebra. It is natural to focus our attention at the main theorem of algebra which states that every n-degree polynomial has exactly n roots (possibly complex numbers). Practical applicability (if reasonable) might ensue from the digit-recurrence (or shift-and-add, or digit-by-digit) nature of the procedure we offer. It is a rule without any exceptions that all digit-recurrence algorithms are hardware-oriented. On the other hand digit-recurrence methods for an implicit functions computation are a great rarity. Nevertheless a standard digit-recurrence procedure for the computation of a located root of a polynomial already exists. It is well-known and it is based on Horner's method [10].
We shall not give Meggitt's results from [10] in detail here. Only some important features of his
method will be discussed. Meggitt replaces the direct computation of the binomial
coefficients of the type
with a simple scheme of shifters and full-precision parallel
adders. The complexity of his method is comparable to the complexity of Horner's
rule evaluation of the polynomial if iterative multipliers not using any acceleration
technique are employed. ( Such multipliers have been out of date for tens of
years. Before jumping into a hasty conclusion the reader should remember that
we discuss procedures for extracting polynomial's roots, not for evaluation
of polynomial values ).
Meggitt offers trial-and-error and non-restoring schemes for his method. No attempt to introduce redundancy has been made. So the question of using the redundant number system {-1. 0, 1} and a carry-save addition instead of the carry-propagate addition remains open. And finally even if the redundant number system {-1, 0, 1} is introduced it is impossible to build recurrences suitable for an on-line computation procedure. The main obstacle seems to be the continued-sum representation of the root.
The continued-product representation of numbers has been utilized for a long time. In 1624 Briggs used it to generate his table of logarithms. Many digit-recurrence algorithms in computer arithmetic are based on a continued-product representation of the argument or the value of a certain function [4].
We suppose that
is an n-degree polynomial with real coefficients
(15)
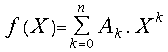and the root is represented as a continued-product
(16)
.
Without loss
of generality we accept that 
for all 
. It can easily be estimated that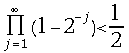 
and 
. Consequently we limit the range of the root values: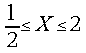
for the digit sets {-1, 1} and {-1, 0, 1};
and 
for the digit set { 0, 1}. We
define:
(17)
;
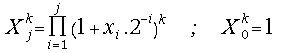(18)
for all and j = 1, 2, 3, ...
The equations
(17) are not needed for the implementation of the algorithm. We derive two sequences
of recurrence equations for
and
,, straightforwardly:
(19)
=
= 
;
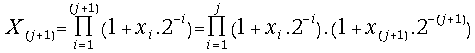(20)
=
=
=
=
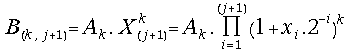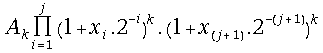for all j = 0, 1, 2, 3, ...
The multiplication
of by 
is implemented as k consecutive shift-and- add operations. The longest
chain of n shift-and-add operations
is needed for the computation of
. At the end of the iteration step we can compute
the value:
(21)
.
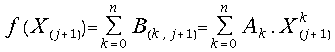The computations
of the recurrences (19), (20) and the equation (21) can be overlapped in time.
More details about the organization of this overlapped computation process will
be given in the next section. Our next assumption is that a selection rule
(22)
exists such that if
, then 
, so
is the root of the polynomial. For the classical trial-and-error
procedure, for the non-restoring scheme and for the redundantly represented
root case we propose the following selection rules:
(23) 
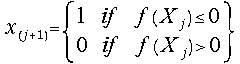for j = 0, 1, 2, 3, ....
(24) 
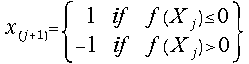for j = 0, 1, 2, 3, ..
(25) 
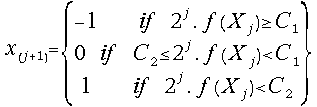for j = 0, 1, 2, 3, ...
The easiest
choice for the selection rule (25) seems to be as close as possible to the standard
radix-2 SRT-division rule. The traditional values of the comparison constants
in (25) are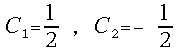
. It is crucial to observe that the first derivative of the polynomial
must be negative near the distinct
real root 
. If the first derivative is positive, then the values of the chosen digits
in the selection rules (23), (24) and (25) must be inverted.
Obviously some additional information about the sign of the first derivative
has to be supplied one way or another.
The equations
(19), (20), (21) and one of the selection rules (23), (24) or (25) define a
digit-recurrence shift-and-add algorithm. It is worth mentioning that the recurrences
are built for the values
, not for the function
. Notice that we compute a residual quantity at the end of each iteration step. If we compare the consecutive
valuesand
and make a decision about the next result digit in a way ensuring
the decrease of
, then the checking of the convergence would be direct. Instead
of this only the sign ofis taken into consideration, when the result digit is chosen. Consequently
the new method uses indirect convergence checking.
The time complexity
of the new method is 
. Within each iteration step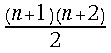 
additions and
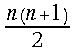variable number of digits shift operations are employed. The same
number of additions and shifts is needed in Meggitt's method. This is a surprising
coincidence since the two methods are derived on the basis of an entirely different
representation of the polynomial's root.
