5. Discussion

Of course proving the convergence of computations for our new methods is the core of the problem. We pleaded guilty at the very beginning confessing that we were not interested in the practical implementation of the proposed new algorithms. However it is our duty to lay out any ideas useful for estimating the range of convergence of the operands or any hints which might lead to establishing the convergence criterions no matter how vague these ideas or hints are.

Obviously the fully on-line algorithm for solving linear systems of algebraic equations is an explicit function computation. Hence it is easier to analyze compared to the on-line method for polynomials. We shall demonstrate how hopelessly impractical the on-line method for solving linear systems may be in the general case. Let us put down for further argument the first scalar equation from (13). The other scalar equations can be treated in the same way:

(31)

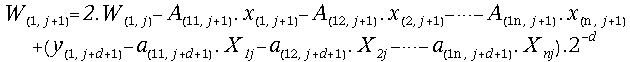
The immediate observation is that (31) contains a large number of addition operations and its implementation is much time- and area-consuming. Next we rewrite the recurrence equation for the simple on-line division of two numbers [8]:

(32).

Taking into account the fact that the convergence criterion of the original E-method requires,, (31) can be viewed as a division procedure with a divisor, a quotient digitand the quantity

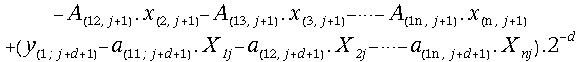
is a "modification" of the shifted residualat the (j+1)-th iteration step. This interpretation of (31) follows strictly the structure of the on-line division equation (32), where the shifted partial remainderis "modified" with the quantityat each iteration step.

We have developed a simple radix-2 division scheme model for recurrences of the type (31) or (32) which is based on the selection rule (14) and formalizes the digital feedback-loop principle [12] ignoring the specific kind of the recurrence equation of a particular algorithm. This division scheme model will not be discussed here but it is worth mentioning that it covers not only on-line computations. The division scheme is also a natural replacement for Muller's decomposition theorems [13] in the shift-and-add methods if the redundant number system {-1, 0, 1} is used.

After the application of the division scheme model to (31) the following condition for convergence of the division procedure is obtained:

(33)

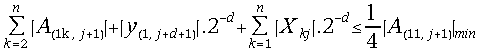
The inequality (33) imposes heavy restrictions on the domain range of the operands even for small values of n if the matrix of the system consists of nonzero elements only. Evidently the diagonal element of the matrix dominates strongly in absolute value over the other elements of the row . So a rough approximation of the solution component can be computed by simply dividing the right-hand side component by( on-line or off-line, that is irrelevant ). Here is a numerical example satisfying (33) that converges for the on-line delay:

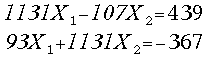
For matrices having large number of zero elements (band matrices for example) the condition (33) is simple and quite manageable. Therefore the new fully on-line method for solving linear systems of algebraic equations becomes reasonable for such matrices.

To analyze the convergence of the system we treated the equations separately from each other here having taken for granted that the matrix of the system is nonsingular. We join the opinion that "ugly mathematics can leave no durable traces in this world". By all means the strict convergence criterion should be established in a matrix form, the way the recurrences were derived in section 2.2. Hence the problem of proving the convergence of the fully on-line method for solving linear systems of algebraic equations remains open.

We have never tried to establish the convergence criterion for our new polynomial methods. We took the numerical example from Meggitt's paper [10], namely:

and we applied the new algorithms to it. The exact solution of the equation is . For the on-line algorithm was chosen. The computations for the new methods converged as expected.

In section 3 the methods of solving linear systems of algebraic equations and computing real roots of polynomials were treated as a generalization of the simple division of two numbers. Such an approach can be easily justified within the framework of the digital feedback-loop principle. It is well-known that the feedback-loop principle plays a fundamental role in cybernetics . Usually the control systems stability is achieved on the basis of their closed-loop structure.

Ensuring convergence of a numerical method of computation may be thought as ensuring stability of a control system. Keeping the residual within a certain range in a method of computation is analogous to tracing the misalignment in a control system.

Our topic is focused on the simplest case of computer arithmetic algorithms in radix-2 number system. As far as we know the digital feedback-loop principle was recognized for the first time as a basic principle in computer arithmetic by G.L.Haviland and A.A.Tuszynski in their version of the CORDIC method [12]. It is easy to observe that practically all digit-recurrence ( or shift-and-add, or digit-by-digit ) methods of the computer arithmetic possess division-like properties. These methods are in fact division-like procedures. The observation becomes quite obvious if an SRT-division selection rule is used to generate the result digits in a digit-recurrence algorithm.

The division of numbers occupies the central part in our discussion because it is the simplest arithmetic operation having a closed-loop structure. The division procedure may be viewed as follows: at each iteration step the one-digit-left shift of the scaled partial remainder is considered as a displacement of its absolute value. Subtracting the divisor from the scaled partial remainder can be considered as a regulating action keeping the absolute value of the partial remainder within a certain range. In general the shift-and-add methods are based on recurrence equations which contain additional modifications of the residuals. These additional modifications are in fact additional misalignment of the absolute value of the residuals and they should be compensated by subtracting the divisor from the residuals.