|
|
Creating a shift-and-add method of solving linear systems of algebraic equations inevitably requires the use of a redundant number system. There exists only one such method described in literature: the well-known evaluation E-method proposed by M.D.Ercegovac [5] , [6] . So it is natural that we should try to analyze the E-method and to make an effort to develop it a step forward if possible.
The E-method is based on an iterative digit-by-digit algorithm of solving a system of linear algebraic equations:
(1) 
.
The elements
of the solution vector
are generated in an on-line manner but a full-precision representation
of the elements of the coefficient matrix
and the elements of the right-hand side vector
is needed in order to initiate the computations.
We are interested in deriving the recurrence equations mainly. As stated by Ercegovac "the on-line arithmetic realizes by definition a variable-precision arithmetic with a built-in significance indication" [7]. Keeping this in mind we could afford not to specify the precision of the operands and the results of an on-line algorithm.
If n is the order of the system (1) then we can define the coefficient matrix
and the right-hand side vector
.
It is necessary to define some additional values related to the solution vector
as follows:
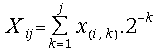is the j digit representation of the i-th component of
the solution vector with all the digits 
belonging to the redundant digit set {-1, 0, 1 };
is the j digit representation of the solution vector;
is the vector of the j-th most significant digits of the
solution components 
, i = 1, 2, ... , n.
From these definitions it follows immediately that
(2) 
.
Next we introduce the residual vectors:
.
We define
(3) 
.
Suppose we have found a selection rule:
(4) 
such that if 
,then 
. In this case we shall receive 
and 
will be the solution vector of the system (1). From (2) and (3)
we can derive recurrence equation for the residual vectors 
:
(5) 
;
; 
, j = 0, 1, 2, ...
Now we introduce the scaled residual vectors 
after M.D.Ercegovac:
(6) 
.
From (5) and (6) we obtain
(7) 
;
, j = 0, 1, 2, ...
If the selection rule 
exists then another selection rule 
can be found
(8) 
Now it is easy to observe that the algorithm consists
of n scalar recursions performed at each iteration step in parallel and described
by (7), and n simultaneously performed selection procedures interleaved with
the recursions and defined by (8). The recursions are based on simple operators:
one digit left shift and a carry-save addition of operands. In fact the selection
of the result digits 
is done by rounding a truncated version of the scaled residuals 
containing only a few of their most significant
digits. The convergence of the E-method was proved by Ercegovac in his Ph.D.
Dissertation. It is important to note that the diagonal elements of the matrix
should prevail strongly in absolute
value over its other elements.
